For a set of destinations, finding the route that gives the smallest length is the well known Traveling Salesman Problem, a combinatorial optimization problem.
For a reduced number of stops, there is no difficulty in looking at all possible combinations. This becomes impossible with increase of the number of destinations because of the factorial relationship between them and the number of routes. For example, for only 12 destinations there are 39,916,800 possible itineraries.
A way to solve this problem, with no guarantee to find the best path, but at least a good one, is inspired on the behavior of ants. Proposed by Dorigo in 1993, it takes the dynamics of pheromones as a mean of selecting the shortest route.

In this post I present my implementation of the ant system in Python. An application to a real world problem will show you how to use ants to plan your next route trip.
Ant system algorithm
The principle is quite simple: ants leave pheromones when they walk, creating a trail. The more ants pass by a given location, more pheromone is accumulated. When comparing two different paths that connect an origin to a destination, a bigger number of ants can pass to the shortest one, so, more pheromone is accumulated. These pheromones attracts more ants, thus, the best (shortest) path is found.
At the start of the solution, multiple agents (ants) are positioned randomly on different nodes (destinations). Initially, all paths have the same level of pheromone. The most crucial part of the algorithm is when an ant selects the direction is going to take next. The choice of the next node is based on the quantity of pheromone and the visibility \(\eta_{ij}\) (inverse of the path length). The probability of selecting path from node \(i\) to \(j\) is defined as:
\(p^k_{ij}(t) =
[ \tau_{ij} ]^\alpha [ \eta_{ij} ]^\beta /
( \sum_{\mathrm{allowed~} k} [ \tau_{ik} ]^\alpha [ \eta_{ik} ]^\beta )
\)
where \(\alpha\) and \(\beta\) are the coefficients indicating the importance of the trail and of the visibility, respectively. Since the objective is to solve a TSP, a route must be defined without repeating any destination, so the probability to go to a node already visited by an ant in the current cycle is null. Quantity \(\tau_{ij}\) is the level of pheromone, accumulated after every time an ant passes by a given \(i\) to \(j\) path:
\(\Delta \tau^k_{ij} =
Q / L_k
\)
with \(L_k\) as the length of the tour by \(k^{th}\) ant on the cycle, so the ants that walk more leave less pheromone per length, and \(Q\) is a constant to define the amount of trail laid by ants. After every cycle, the trail quantity is updated (\(\rho\) is the trail persistence coefficient):
\( \tau_{ij} =
\rho \tau_{ij} + \sum_k \Delta \tau^k_{ij}
\)
Once all ants have visited all node, we move to the next cycle where they are once more placed randomly on a node and a new cycle is defined. The full description of the algorithm is available on the original paper. You can also check my implementation, more details on the end of this post.
As a canonical problem, many benchmarks exist. The TSPLIB library by Gerhard Reinelt from the University of Heidelberg, is a very complete compilation of different set of nodes, including different metrics and the best route for some of them.
I performed a parametric study of my own for the ant system parameters (\(\alpha\), \(\beta\), \(\rho\), \(Q\) and number of ant \(m\)) using the Oliver30 (as in Dorigo’s article) and Berlin52 nodes. The ant system parameters listed on the original article (\(\alpha = 1.0\), \(\beta = 5.0\), \(\rho = 0.5\) and \(Q = 100\)) are already the optimal, thus, used on this analysis. In terms of the number of ants, twice the number of nodes is picked (\(m = 2 n\)).
Animations with the solution for the Oliver30 benchmark illustrates the fast convergence of the algorithm.
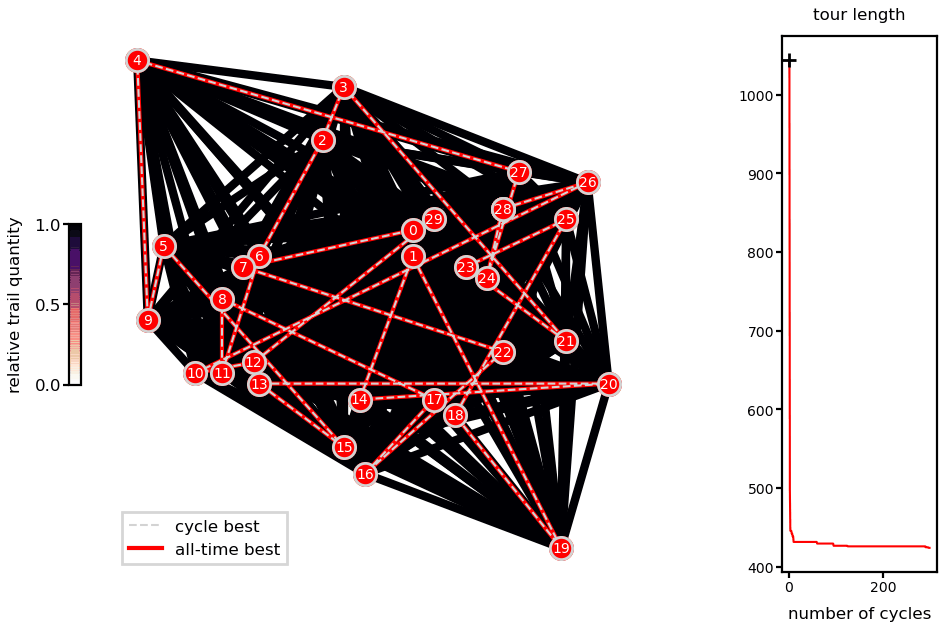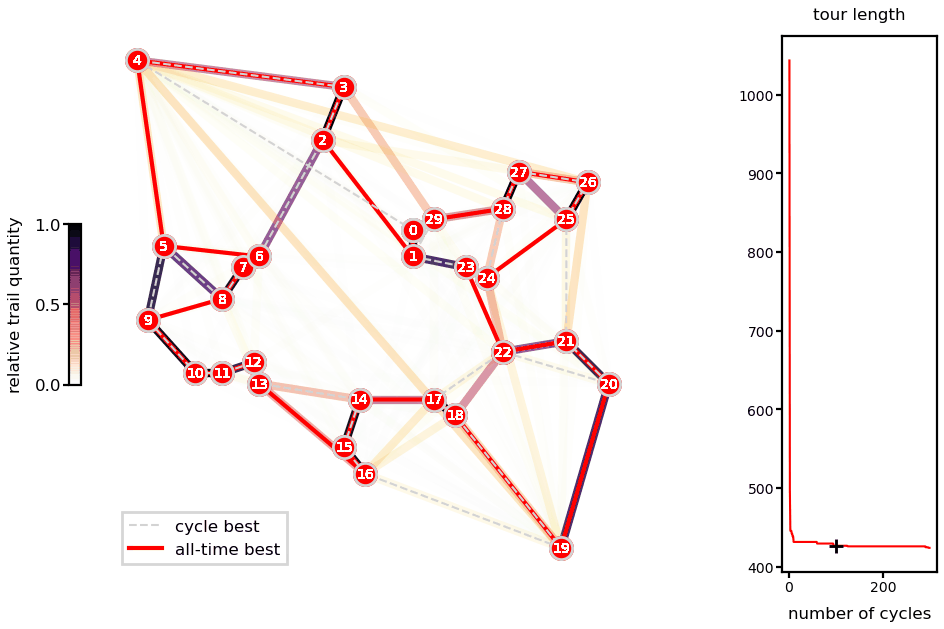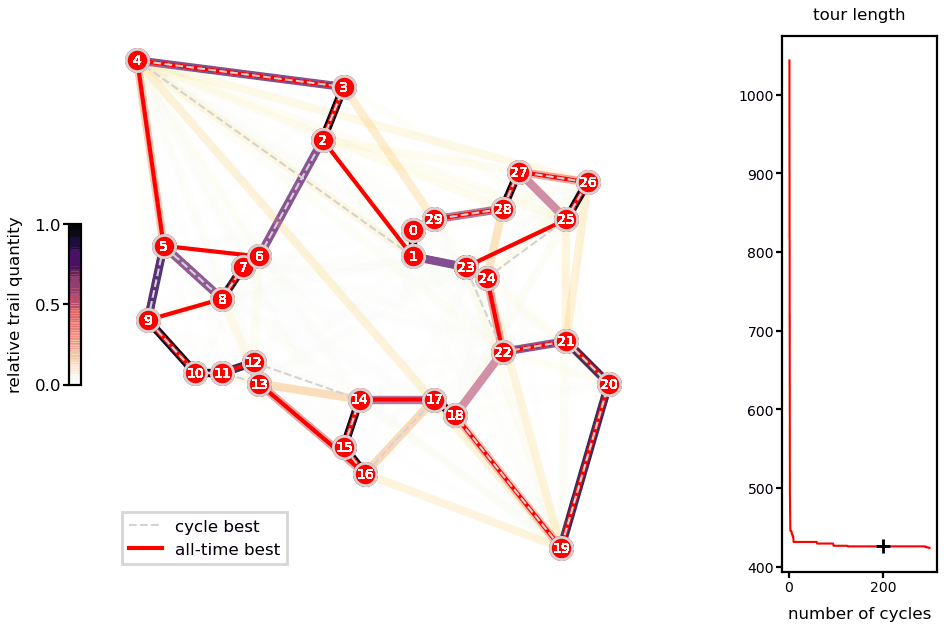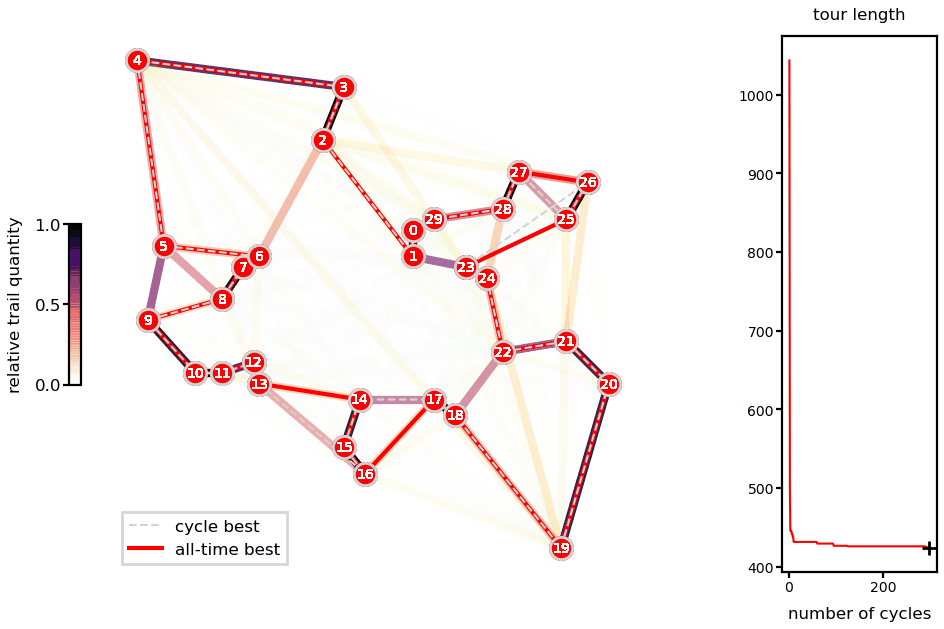
Ant system solution of the Oliver30 problem.
As a heuristic method, there is no guarantee of finding the global minimum and different runs lead to different solutions (unless you fix the random number generator seeds). Nevertheless, presented runs are very close to reported best (difference of 0.04% for the Oliver30 case).
If you are interested, there are many other nature inspired algorithms exist, such as Particle Swarm Optimization (PSO), inspired by the dynamics of flocks of birds, and Genetic Algorithm (GA), derived from the principle of evolution, where the fittest remain and reproduce. An application of the former can be found on my PhD manuscript.
Real world application
A straightforward application of the optimization algorithm is to plan a road-trip. This is far from any hard and complex problem such as to define the route of a deliver truck, but is a fun application anyone can relate to. Once the cities I picked are not very close it is not complicated to find an optimal solution, different from the benchmarks that are hard on purpose.
Considering latitude and longitude of the cities and a given earth radius would be possible but not that close to reality, because natural obstacles such as mountains and lakes are ignored, changes in route length due to elevation are not considered as well, and finally, you cannot drive where there are no roads.
So, from a list of destinations, I need to get the routes between them. It is possible to use Google Maps, but the route is limited to 10 destinations (nothing stops you to start over from where you left, but this was not my objective). You probably can do a lot more with Google API, but anyway, the Openrouteservice API, an open source route planner, is used to obtain the itineraries. Also, I wanted to code, so any other solutions would not make me not do it myself.
Openrouteservice API has its own TSB (actually Vehicle Routing Problem – VRP) algorithm, so use theirs if you really want to plan a trip. They have a nice example for a pub crawl. Mine its just me playing around and coding.
In order to get the matrix of distances \(d_{ij}\), I requested the directions considering all possible A to B combinations (when the origin is the same as the destination the distance is null, obviously). I consider that the problem is symmetric (going from A to B is the same as going from B to A). More details on the last section of this post.
Three applications of growing complexity are performed: traveling to all regions capitals of metropolitan France (13 cities), the states capitals of Brazil (27 cities) and the capitals of Europe (48 cities).
French capitals (\(n = 13\))
Metropolitan France is composed by 13 regions. From Openrouteservice, these are the obtained driving distances in kilometers:
|
Lyon
|
Dijon
|
Rennes
|
Orleans
|
Ajaccio
|
Strasbourg
|
Lille
|
Paris
|
Rouen
|
Bordeaux
|
Toulouse
|
Nantes
|
Marseille
|
|
| Lyon | 0 | 192 | 735 | 446 | 710 | 488 | 690 | 464 | 594 | 553 | 538 | 684 | 315 | Dijon | 192 | 0 | 618 | 315 | 902 | 330 | 502 | 314 | 444 | 718 | 721 | 640 | 507 |
| Rennes | 735 | 618 | 0 | 345 | 1444 | 829 | 569 | 347 | 307 | 461 | 699 | 107 | 1049 |
| Orleans | 446 | 315 | 345 | 0 | 1155 | 604 | 352 | 131 | 239 | 461 | 553 | 334 | 760 |
| Ajaccio | 710 | 902 | 1444 | 1155 | 0 | 1022 | 1397 | 1171 | 1300 | 1042 | 803 | 1384 | 442 |
| Strasbourg | 488 | 330 | 829 | 604 | 1022 | 0 | 553 | 492 | 637 | 1017 | 1020 | 865 | 809 |
| Lille | 690 | 502 | 569 | 352 | 1397 | 553 | 0 | 221 | 254 | 804 | 898 | 604 | 1004 |
| Paris | 464 | 314 | 347 | 131 | 1171 | 492 | 221 | 0 | 136 | 584 | 677 | 384 | 778 |
| Rouen | 594 | 444 | 307 | 239 | 1300 | 637 | 254 | 136 | 0 | 653 | 784 | 385 | 906 |
| Bordeaux | 553 | 718 | 461 | 461 | 1042 | 1017 | 804 | 584 | 653 | 0 | 243 | 349 | 648 |
| Toulouse | 538 | 721 | 699 | 553 | 803 | 1020 | 898 | 677 | 784 | 243 | 0 | 587 | 408 |
| Nantes | 684 | 640 | 107 | 334 | 1384 | 865 | 604 | 384 | 385 | 349 | 587 | 0 | 991 |
| Marseille | 315 | 507 | 1049 | 760 | 442 | 809 | 1004 | 778 | 906 | 648 | 408 | 991 | 0 |
Paris → Orléans → Rennes → Nantes → Bordeaux → Toulouse → Marseille
→ Ajaccio (ferry necessary!) → Lyon → Dijon → Strasbourg → Lille → Rouen → Paris

directions from © openrouteservice.org by HeiGIT | Map data © OpenStreetMap contributors
Brazilian capitals (\(n = 27\))
There are 27 state capitals in Brazil (actually 26 because one of them is the capital of the federal district, thus, of the country). On an offsite point on the history of the country, the location of the capitals reflect the colonization process that started on the coast. Also, these regions represent the most important economic poles. Up-to-date, it is where most of the population is concentrated.
Best route I could found was 21,557 kilometers long. Influence of geographical barriers is clear on this example. Direct, straight link between Belem and Manaus is not really possible due to the presence of the Amazon Forrest and the Amazon river. To reach Manaus you need first to go south, almost reaching Porto Velho, than go north in the Transamazon road to arrive in Manaus.

directions from © openrouteservice.org by HeiGIT | Map data © OpenStreetMap contributors
European capitals (\(n = 48\))
Last application considers 48 capitals of european countries. Some were missing:
- Reykjavík, capital of Iceland, because you cannot get there with a car
- Nur-Sultan, capital of Kazakhstan, because its very far and would make the map look ugly
- Pristina, capital of Kosovo, is not considered as well
The optimal route is almost 30 thousands kilometers long, less than half the initial one (random). Like in the previous case, unless you are a truck driver or a very enthusiastic RV driver, it is quite hard to accomplish. This simple code and application examples show the power of the algorithm.

directions from © openrouteservice.org by HeiGIT | Map data © OpenStreetMap contributors
More refined methods and complex cases, like when time, traffic, vehicle maintenance and driver schedules, fueling stations locations, weather, and many other parameters are taken in account, can result in even more gains.
Under the hood
Full implementation, including the ant system algorithms and post processing scripts are available here and in my Github organization. If you want to play around or plan a trip of you own, keep in mind that there are no warranties!
Choice from custom probability distribution
I have not focused on optimizing the code, only one aspect was tested: the selection of a random number from a custom probability distribution. There are two straightforward options to use: Python’s random.random.choices and Numpy’s numpy.random.choice.
For the Python’s option, you can either give the distribution (weights) or the cumulative distribution (cum_weights) as argument. When you check the random module source code, you can see clearly that the cumulative distribution is the one that is actually used, when you give the distribution itself as an argument it is calculated inside.
if cum_weights is None:
if weights is None:
# ...
cum_weights = list(_accumulate(weights))
Giving the cumulative distribution as input reduces the time of the function call drastically, but if you account the time used to calculate the cumulative distribution, the total time is basically unchanged.
Numpy’s solution, contrary to my expectation, is way less efficient. From the numpy’s choice source code you can see that the same core operations of the Python version are performed. The loss in performance is probably associated with the overhead of the function call.
On both cases, a lot of time is used to check the inputs. My solution to improve the performance a bit was to simplify them by removing all these checks (I have done it for both Python’s and Numpy’s choice functions, only the later is showed next):
def simple_np_choices(self, population, cum_weights, k=1):
""" Simplified version of the numpy.random.choice function """
uniform_samples = np.random.random(k)
return population[int(
cum_weights.searchsorted(
uniform_samples,
side='right'
)
)
]
For 100 thousands selections with a population of 100, execution time was reduced from almost 4 to 0.6 seconds. Numpy’s simplified code is slightly better than the Python’s version.

Obtaining the routes
Directions between the cities are obtained using the free Openrouteservice API, more specifically, their Python implementation. You only need to create an account to get an API key. The Pelias geocoder, integrated to Openrouteservice, is used to get the coordinates of the cities.
You are limited to 40 requests per minute, 2,000 a day, so I split the solution into two steps. First, I use pairs of origin to destination to get the directions. If you only need the matrix of distances \(d_{ij}\), distance_matrix method can be used, but you will not get the directions connecting the cities. A *.npz file is saved with the destinations information, the directions and the distance matrix. Another script load this file, solves the TSP problem and plots the maps.
Maps production
For map production, cartopy library was used. Country information is from Natural Earth and regions are from the GADM database; the Robinson projection is used.
Everything here was made using open source and free solutions. Hope it motivates you to consider the alternatives to the current dominant solutions and give a chance to open source! Feel free to contact me and send your questions/corrections/comments!